Artificial dataset A


5.3. Artificial datasets with feature selection
|
Artificial dataset A
|
Artificial dataset
B
|
In the previous section 5.1., we showed that, using the same number of dimensions, there is no reason to prefer
ICA over whitened data.
However, the performance of ICA and PCA may differ when a subset
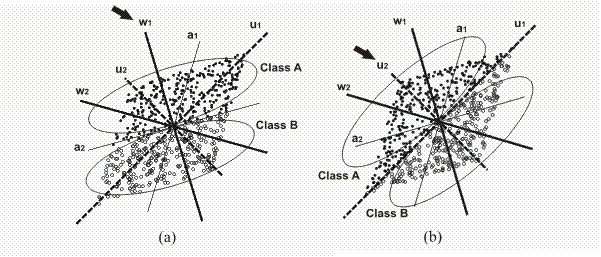
of components is used for classification. To illustrate this fact, in the two extreme examples of artificial sets (A and B) we have drawn the directions of the eigenvectors, U, and the ICA directions, W and A.As both techniques are unsupervised, these directions are independent from the classes in the data set, so they are equal for both extreme examples.
In figure (a) it is easy to appreciate how the classes are perfectly separated using just the projection over the ICA direction w1, while in (b), the classes are better separated using the direction of eigenvector u2. Therefore, in each example, a feature selection step may help to reduce the dimensionality and improve the classification. If no feature selection is carried out, ICA and whitened PCA perform exactly equally well on both datasets, provided a rotationally symmetric classifier is used.
 |
In the following experiments you must edit the "example.m" function and modify some parametes in order to obtain the same results that are shown here. (In each experiment, the modified parameter is highlighted
With the feature selection parameter set, the matlab code is limited to 8 components due to computational time costs.
EXPERIMENT 13
Artificial dataset A and FASTICA (with feature selection)
nc=2; %number of classes
np=300; %number of samples per class
n_vectors=2; %number of vectors used to reduce the data
nr=2; %number of repetitions of the classification process
per_test=0.5; %percentage of test samples from x (0-1)
Legend ------------------->
>> example(1,1,1)
 |
 |
 |
 |
EXPERIMENT 14
Artificial dataset B and FASTICA (with feature selection)
nc=2; %number of classes
np=300; %number of samples per class
n_vectors=2; %number of vectors used to reduce the data
nr=2; %number of repetitions of the classification process
per_test=0.5; %percentage of test samples from x (0-1)
>> example(2,1,1)
 |
 |
 |
 |
EXPERIMENT 15
Artificial dataset A and Infomax (with feature selection)
nc=2; %number of classes
np=300; %number of samples per class
n_vectors=2; %number of vectors used to reduce the data
nr=2; %number of repetitions of the classification process
per_test=0.5; %percentage of test samples from x (0-1)
>> example(1,2,1)
 |
 |
 |
 |
EXPERIMENT 16
Artificial dataset B and Infomax (with feature selection)
nc=2; %number of classes
np=300; %number of samples per class
n_vectors=2; %number of vectors used to reduce the data
nr=2; %number of repetitions of the classification process
per_test=0.5; %percentage of test samples from x (0-1)
>> example(2,2,1)
 |
 |
 |
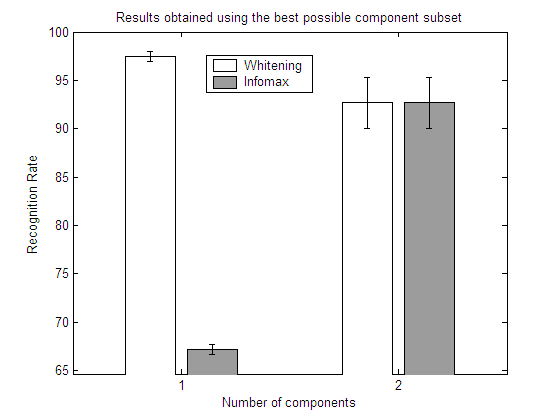 |
CONCLUSIONS (Experiments 13-16)
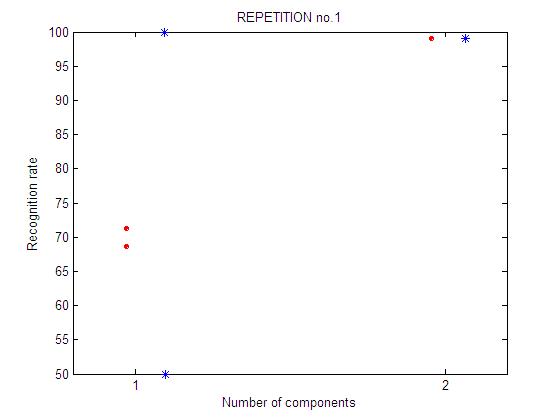
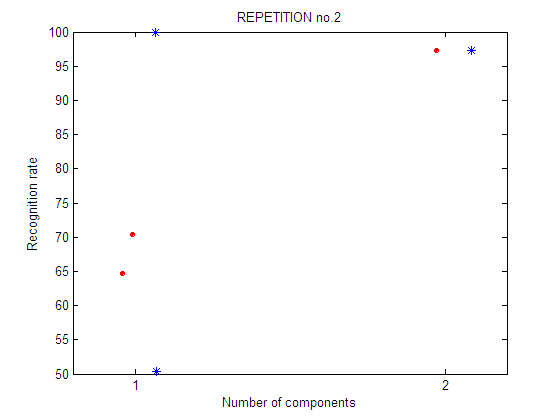
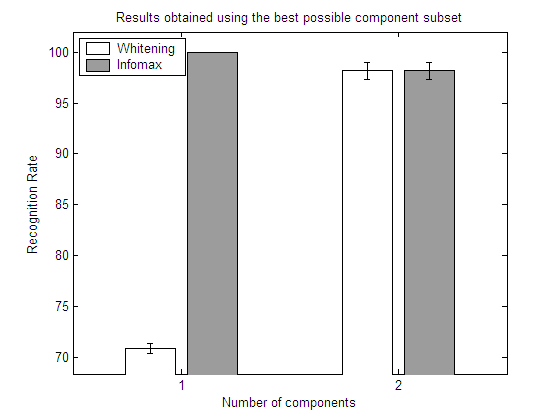
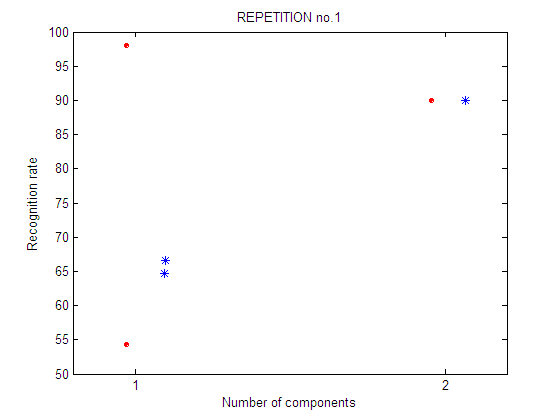
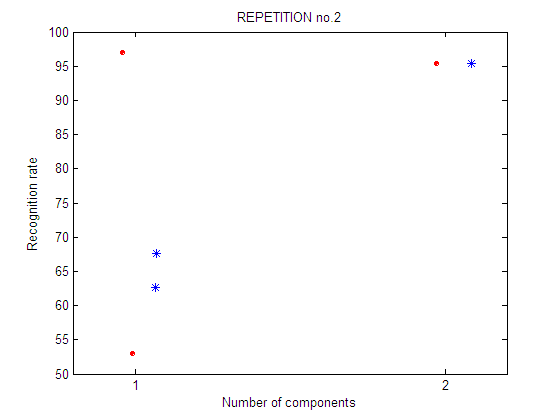
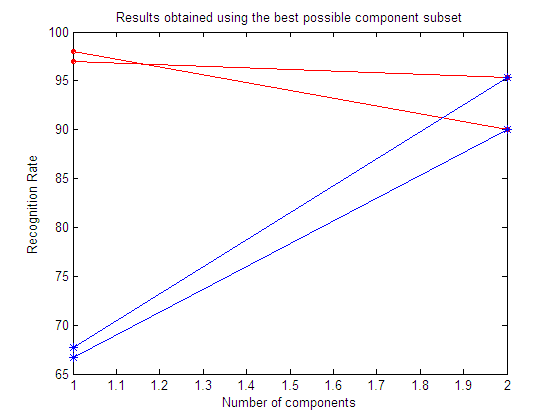
In each experiment, 4 plots are shown:
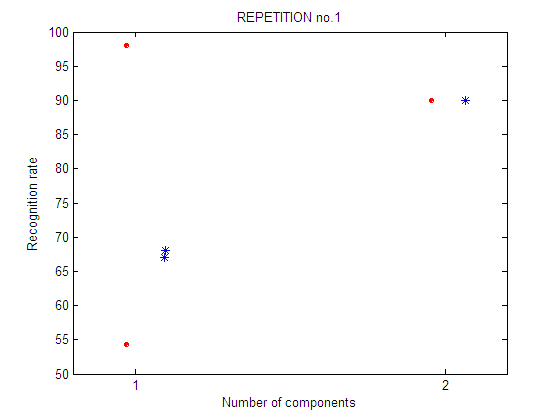
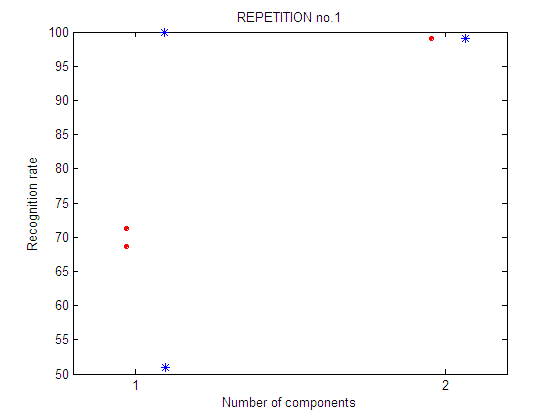
| repetition 1
First repetition of the feature selection experiment. For each number of components an exhaustive feature selection process is carried out. It means that all the subsets of n-components are tested. There are 2 possible subsets of 1 component and only 1 possible subset of 2 components.
|
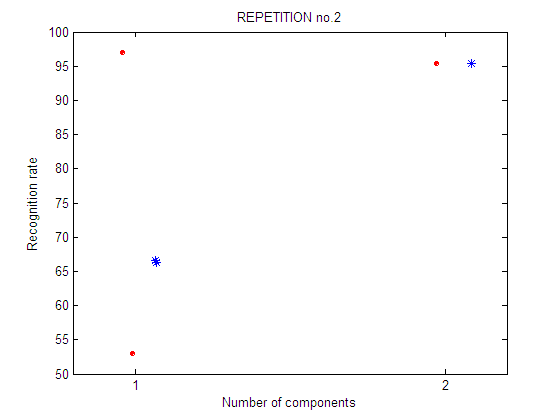
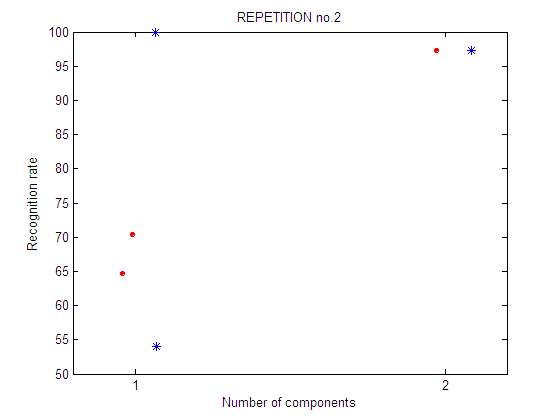
repetition 2
Second repetition of the feature selection experiment. A different selection of training and test sets is used. Legend:
|
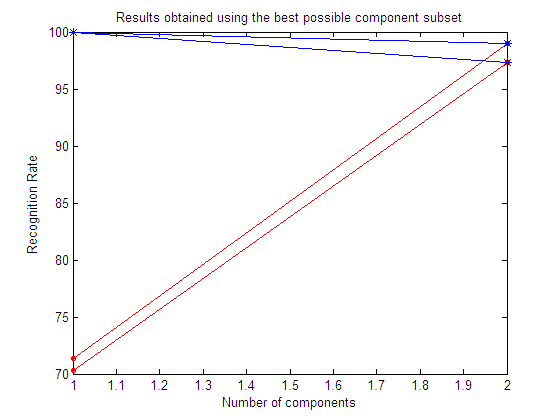
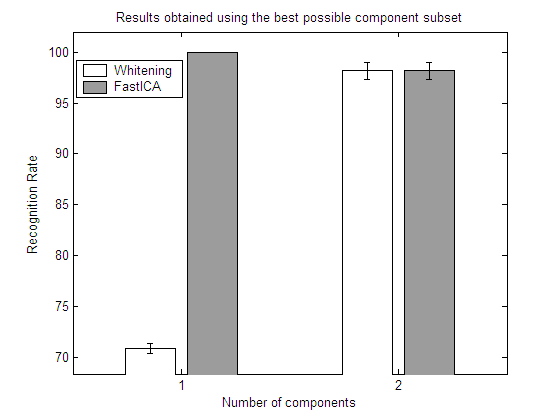
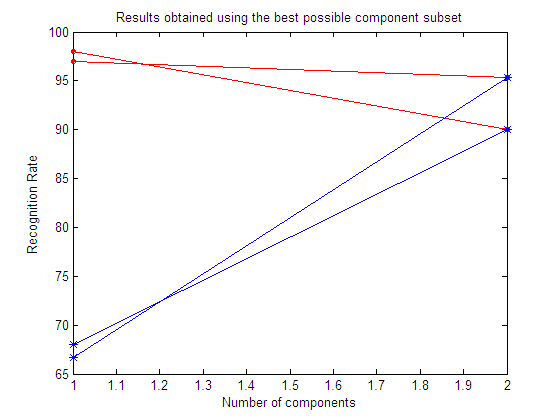
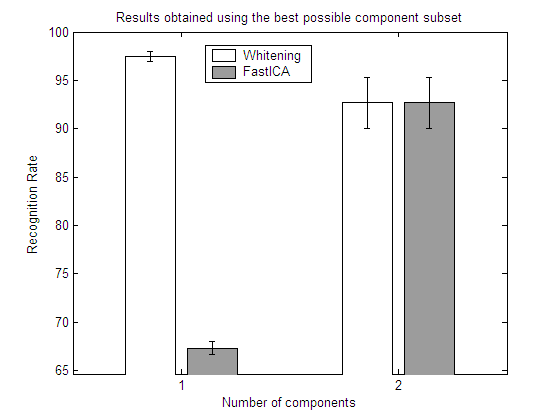
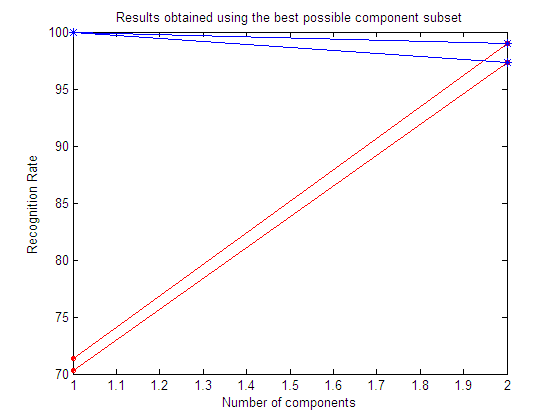
| Results obtained using the best possible
component subset
Here we show the best subset in each repetition.
|
Results obtained using the best possible
component subset
Here we show the mean value of the best subset among all the repetitions.
|
From the results in the above experiments it is easy to see how a feature selection step may help to reduce the dimensionality and improve the classification results. Depending on the particular dataset, ICA may or may not outperform whitened PCA.